Adopted lfs_ctz_index implementation using popcount

This reduces the O(n^2logn) runtime to read a file to only O(nlog).
The extra O(n) did not touch the disk, so it isn't a problem until the
files become very large, but this solution comes with very little cost.

Long story short, you can find the block index + offset pair for a
CTZ linked-list with this series of formulas:

n' = floor(N / (B - 2w/8))
N' = (B - 2w/8)n' + (w/8)popcount(n')
off' = N - N'
n, off =
  n'-1, off'+B                if off' <  0
  n',   off'+(w/8)(ctz(n')+1) if off' >= 0

For the long story, you will need to see the updated DESIGN.md

DESIGN.md

@@ -290,31 +290,32 @@ The path to data block 0 is even more quick, requiring only two jumps:
 
 We can find the runtime complexity by looking at the path to any block from
 the block containing the most pointers. Every step along the path divides
-the search space for the block in half. This gives us a runtime of O(log n).
+the search space for the block in half. This gives us a runtime of O(logn).
 To get to the block with the most pointers, we can perform the same steps
-backwards, which keeps the asymptotic runtime at O(log n). The interesting
+backwards, which puts the runtime at O(2logn) = O(logn). The interesting
 part about this data structure is that this optimal path occurs naturally
 if we greedily choose the pointer that covers the most distance without passing
 our target block.
 
 So now we have a representation of files that can be appended trivially with
-a runtime of O(1), and can be read with a worst case runtime of O(n logn).
+a runtime of O(1), and can be read with a worst case runtime of O(nlogn).
 Given that the the runtime is also divided by the amount of data we can store
 in a block, this is pretty reasonable.
 
 Unfortunately, the CTZ skip-list comes with a few questions that aren't
 straightforward to answer. What is the overhead? How do we handle more
-pointers than we can store in a block?
+pointers than we can store in a block? How do we store the skip-list in
+a directory entry?
 
 One way to find the overhead per block is to look at the data structure as
 multiple layers of linked-lists. Each linked-list skips twice as many blocks
-as the previous linked-list. Or another way of looking at it is that each 
+as the previous linked-list. Another way of looking at it is that each 
 linked-list uses half as much storage per block as the previous linked-list.
 As we approach infinity, the number of pointers per block forms a geometric
 series. Solving this geometric series gives us an average of only 2 pointers
 per block.
 
-![overhead per block](https://latex.codecogs.com/gif.latex?%5Clim_%7Bn%5Cto%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D0%7D%5E%7Bn%7D%5Cleft%28%5Ctext%7Bctz%7D%28i%29+1%5Cright%29%20%3D%20%5Csum_%7Bi%3D0%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B2%5Ei%7D%20%3D%202)
+![overhead_per_block](https://latex.codecogs.com/svg.latex?%5Clim_%7Bn%5Cto%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D0%7D%5E%7Bn%7D%5Cleft%28%5Ctext%7Bctz%7D%28i%29+1%5Cright%29%20%3D%20%5Csum_%7Bi%3D0%7D%5Cfrac%7B1%7D%7B2%5Ei%7D%20%3D%202)
 
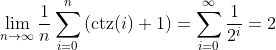
 Finding the maximum number of pointers in a block is a bit more complicated,
 but since our file size is limited by the integer width we use to store the
@@ -322,7 +323,7 @@ size, we can solve for it. Setting the overhead of the maximum pointers equal
 to the block size we get the following equation. Note that a smaller block size
 results in more pointers, and a larger word width results in larger pointers.
 
-![maximum overhead](https://latex.codecogs.com/gif.latex?B%20%3D%20%5Cfrac%7Bw%7D%7B8%7D%5Cleft%5Clceil%5Clog_2%5Cleft%28%5Cfrac%7B2%5Ew%7D%7BB-2%5Cfrac%7Bw%7D%7B8%7D%7D%5Cright%29%5Cright%5Crceil)
+![maximum overhead](https://latex.codecogs.com/svg.latex?B%20%3D%20%5Cfrac%7Bw%7D%7B8%7D%5Cleft%5Clceil%5Clog_2%5Cleft%28%5Cfrac%7B2%5Ew%7D%7BB-2%5Cfrac%7Bw%7D%7B8%7D%7D%5Cright%29%5Cright%5Crceil)
 
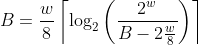
 where:  
 B = block size in bytes  
@@ -335,8 +336,102 @@ widths:
 
 Since littlefs uses a 32 bit word size, we are limited to a minimum block
 size of 104 bytes. This is a perfectly reasonable minimum block size, with most
-block sizes starting around 512 bytes. So we can avoid the additional logic
-needed to avoid overflowing our block's capacity in the CTZ skip-list.
+block sizes starting around 512 bytes. So we can avoid additional logic to
+avoid overflowing our block's capacity in the CTZ skip-list.
+
+So, how do we store the skip-list in a directory entry? A naive approach would
+be to store a pointer to the head of the skip-list, the length of the file
+in bytes, the index of the head block in the skip-list, and the offset in the
+head block in bytes. However this is a lot of information, and we can observe
+that a file size maps to only one block index + offset pair. So it should be
+sufficient to store only the pointer and file size.
+
+But there is one problem, calculating the block index + offset pair from a
+file size doesn't have an obvious implementation.
+
+We can start by just writing down an equation. The first idea that comes to
+mind is to just use a for loop to sum together blocks until we reach our
+file size. We can write equation equation as a summation:
+
+![summation1](https://latex.codecogs.com/svg.latex?N%20%3D%20%5Csum_i%5En%5Cleft%5BB-%5Cfrac%7Bw%7D%7B8%7D%5Cleft%28%5Ctext%7Bctz%7D%28i%29+1%5Cright%29%5Cright%5D)
+
+where:  
+B = block size in bytes  
+w = word width in bits  
+n = block index in skip-list  
+N = file size in bytes  
+
+And this works quite well, but is not trivial to calculate. This equation
+requires O(n) to compute, which brings the entire runtime of reading a file
+to O(n^2logn). Fortunately, the additional O(n) does not need to touch disk,
+so it is not completely unreasonable. But if we could solve this equation into
+a form that is easily computable, we can avoid a big slowdown.
+
+Unfortunately, the summation of the CTZ instruction presents a big challenge.
+How would you even begin to reason about integrating a bitwise instruction?
+Fortunately, there is a powerful tool I've found useful in these situations:
+The [On-Line Encyclopedia of Integer Sequences (OEIS)](https://oeis.org/).
+If we work out the first couple of values in our summation, we find that CTZ
+maps to [A001511](https://oeis.org/A001511), and its partial summation maps
+to [A005187](https://oeis.org/A005187), and surprisingly, both of these
+sequences have relatively trivial equations! This leads us to the completely
+unintuitive property:
+
+![mindblown](https://latex.codecogs.com/svg.latex?%5Csum_i%5En%5Cleft%28%5Ctext%7Bctz%7D%28i%29+1%5Cright%29%20%3D%202n-%5Ctext%7Bpopcount%7D%28n%29)
+
+where:  
+ctz(i) = the number of trailing bits that are 0 in i  
+popcount(i) = the number of bits that are 1 in i  
+
+I find it bewildering that these two seemingly unrelated bitwise instructions
+are related by this property. But if we start to disect this equation we can
+see that it does hold. As n approaches infinity, we do end up with an average
+overhead of 2 pointers as we find earlier. And popcount seems to handle the
+error from this average as it accumulates in the CTZ skip-list.
+
+Now we can substitute into the original equation to get a trivial equation
+for a file size:
+
+![summation2](https://latex.codecogs.com/svg.latex?N%20%3D%20Bn%20-%20%5Cfrac%7Bw%7D%7B8%7D%5Cleft%282n-%5Ctext%7Bpopcount%7D%28n%29%5Cright%29)
+
+Unfortunately, we're not quite done. The popcount function is non-injective,
+so we can only find the file size from the block index, not the other way
+around. However, we can guess and correct. Consider an n' block index that
+is greater than n, we can find one pretty easily:
+
+![summation3step1](https://latex.codecogs.com/svg.latex?n%27%20%3D%20%5Cleft%5Clfloor%5Cfrac%7BN%7D%7BB-2%5Cfrac%7Bw%7D%7B8%7D%7D%5Cright%5Crfloor)
+
+where:  
+n' >= n  
+
+We can plug n' back into our popcount equation to find an N' file size that
+is greater than N. However, we need to rearrange our terms a bit to avoid
+integer overflow:
+
+![summation3step2](https://latex.codecogs.com/svg.latex?N%27%20%3D%20%28B-2%5Cfrac%7Bw%7D%7B8%7D%29n%27+%5Cfrac%7Bw%7D%7B8%7D%5Ctext%7Bpopcount%7D%28n%27%29)
+
+where:  
+N' >= N  
+
+Now that we have N', we can find our block offset:
+
+![summation3step3](https://latex.codecogs.com/svg.latex?%5Cmathit%7Boff%7D%27%20%3D%20N%20-%20N%27)
+
+where:  
+off' >= off, our byte offset in the block  
+
+Now we're getting somewhere. N' is greater than or equal to N, and as long as
+the number of pointers per block is bounded by the block size, it can only be
+different by at most one block. So we have two cases that can be determined by
+the sign of off'. If off' is negative, we correct n' and add a block to off'.
+Note that we also need to incorporate the overhead of the last block to get
+the right offset.
+
+![summation3step4](https://latex.codecogs.com/svg.latex?n%2C%20%5Cmathit%7Boff%7D%20%3D%20%5Cbegin%7Bcases%7D%20n%27-1%2C%20%5Cmathit%7Boff%7D%27+B%20%26%20%5Cmathit%7Boff%7D%27%20%3C%200%20%5C%5C%20n%27%2C%20%5Cmathit%7Boff%7D%27+%5Cfrac%7Bw%7D%7B8%7D%5Cleft%5B%5Ctext%7Bctz%7D%28n%27%29+1%5Cright%5D%20%26%20%5Cmathit%7Boff%7D%27%20%5Cgeq%200%20%5Cend%7Bcases%7D)
+
+It's a lot of math, but computers are very good at math. With these equations
+we can solve for the block index + offset while only needed to store the file
+size in O(1).
 
 Here is what it might look like to update a file stored with a CTZ skip-list:
 ```
@@ -1129,7 +1224,7 @@ So, to summarize:
    metadata block is active
 4. Directory blocks contain either references to other directories or files
 5. Files are represented by copy-on-write CTZ skip-lists which support O(1)
-   append and O(n logn) reading
+   append and O(nlogn) reading
 6. Blocks are allocated by scanning the filesystem for used blocks in a
    fixed-size lookahead region is that stored in a bit-vector
 7. To facilitate scanning the filesystem, all directories are part of a